Defines a basic Solver model. Equivalent to clicking Solver in the Data | Analysis group and then specifying options in the Solver Parameters dialog box.
SimplexLP 2 is an app to solve optimization problems, which can be mathematically described as an objective function and a set of constraints in the form of linear inequalities. For the calculation the famous Simplex algorithm is used. Developing the first Row by the key elements 2, the intermediate coefficient matrix is obtained as. This solution as read from this table is x 1 = 3, x 2 = 2, S 1, = 0, S 2 = 0 and Z= 11. Also using the formula Δ j = C B X j – C j verify that all Δ j ‘s are non-negative. Hence the optimum.
SimplexLP 2 makes it incredibly easy to solve linear optimization problems. Just type in the objective function and the constraints as you would write them down on paper. Just click Calculate and get the results instantly. Change coefficients and see how the solution changes. Teachers can very e. 2 R 2 R 1 R 1 2R 2 R 2 1 2 R 2 The new tableau that we obtain is: 3/2 0 -7/2 13/2 0 3/2 2 0 0 0 1 -2 1/2 1 -1/2 1/2 0 1/2 associated with the solution (1=2;0;0;2;0) of aluev z= 3=2. Again, we look at the 0-th row to check the presence of negative reduced costs. We have a single ariablev associated with negative reduced cost, namely x 2.
Before you use this function, you must establish a reference to the Solver add-in. In the Visual Basic Editor, with a module active, click References on the Tools menu, and then select the Solver.xlam check box under Available References. If Solver.xlam does not appear under Available References, click Browse and open Solver.xlam in the office14librarySolver subfolder.
SolverOk(SetCell, MaxMinVal, ValueOf, ByChange, Engine, EngineDesc)
SetCell Optional Variant. Refers to a single cell on the active worksheet. Corresponds to the Set Objective Cell box in the Solver Parameters dialog box.
MaxMinVal Optional Variant. Corresponds to the Max, Min, and Value options in the Solver Parameters dialog box.
MaxMinVal | Specifies |
1 | Maximize |
2 | Minimize |
3 | Match a specific value |
ValueOf Optional Variant. If MaxMinVal is 3, you must specify the value to which the target cell is matched.
ByChange Required Variant. The cell or range of cells that will be changed so that you will obtain the desired result in the target cell. Corresponds to the By Changing Variable Cells box in the Solver Parameters dialog box.
Engine Optional Variant. The Solving method that should be used to solve the problem: 1 for the Simplex LP method, 2 for the GRG Nonlinear method, or 3 for the Evolutionary method. Corresponds to the Select a Solving Method dropdown list in the Solver Parameters dialog box.
EngineDesc Optional Variant. An alternate way to specify the Solving method that should be used to solve the problem as a string: 'Simplex LP', 'GRG Nonlinear', or 'Evolutionary'. Corresponds to the Select a Solving Method dropdown list in the Solver Parameters dialog box.
Example

This example uses the Solver functions to maximize gross profit in a business problem. The SolverOK function defines a problem by specifying the SetCell, MaxMinVal, and ByChange arguments.
Worksheets('Sheet1'). Activate SolverReset SolverOptions precision:=0.001 SolverOK SetCell:=Range ('TotalProfit'), _ MaxMinVal:=1, _ ByChange:=Range ('C4:E6') SolverAdd CellRef:=Range ('F4:F6'), _ Relation:=1, _ FormulaText:=100 SolverAdd CellRef:=Range ('C4:E6'), _ Relation:=3, _ FormulaText:=0 SolverAdd CellRef:=Range ('C4:E6'), _ Relation:=4 SolverSolve UserFinish:=False SolverSave SaveArea:=Range ('A33') |
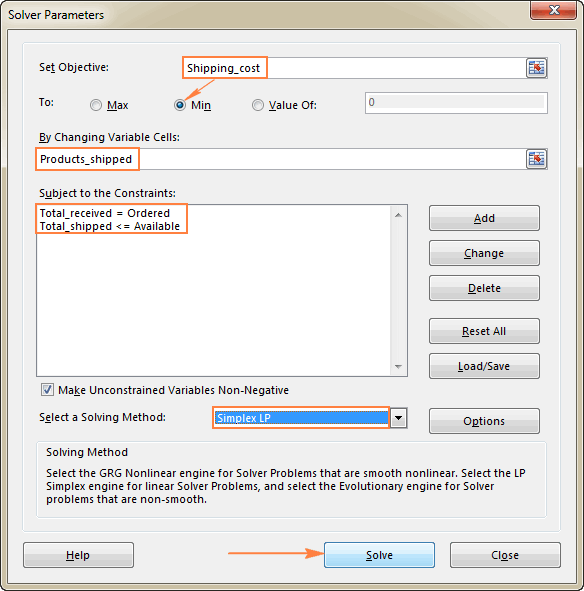
Defines a basic Solver model. Equivalent to clicking Solver in the Data | Analysis group and then specifying options in the Solver Parameters dialog box.
Note The Solver add-in is not enabled by default. Before you can use this function, you must have the Solver add-in enabled and installed. For information about how to do that, see Using the Solver VBA Functions. After the Solver add-in is installed, you must establish a reference to the Solver add-in. In the Visual Basic Editor, with a module active, click References on the Tools menu, and then select Solver under Available References. If Solver does not appear under Available References, click Browse, and then open Solver.xlam in the Program FilesMicrosoft OfficeOffice14LibrarySOLVER subfolder.
SolverOk( SetCell, MaxMinVal, ValueOf, ByChange, Engine, EngineDesc)
SetCell Optional Variant. Refers to a single cell on the active worksheet. Corresponds to the Set Target Cell box in the Solver Parameters dialog box.MaxMinVal Optional Variant. Corresponds to the Max, Min, and Value options in the Solver Parameters dialog box.
| MaxMinVal | Specifies |
|---|---|
| 1 | Maximize |
| 2 | Minimize |
| 3 | Match a specific value |
ValueOf Optional Variant. If MaxMinVal is 3, you must specify the value to which the target cell is matched.
ByChange Optional Variant. The cell or range of cells that will be changed so that you will obtain the desired result in the target cell. Corresponds to the By Changing Cells box in the Solver Parameters dialog box.
Engine Optional Variant. The Solving method that should be used to solve the problem: 2 for the Simplex LP method, 1 for the GRG Nonlinear method, or 3 for the Evolutionary method. Corresponds to the Select a Solving Method dropdown list in the Solver Parameters dialog box.
Simplex Lp1020
EngineDesc Optional Variant. An alternate way to specify the Solving method that should be used to solve the problem as a string: 'Simplex LP', 'GRG Nonlinear', or 'Evolutionary'. Corresponds to the Select a Solving Method dropdown list in the Solver Parameters dialog box.
Example
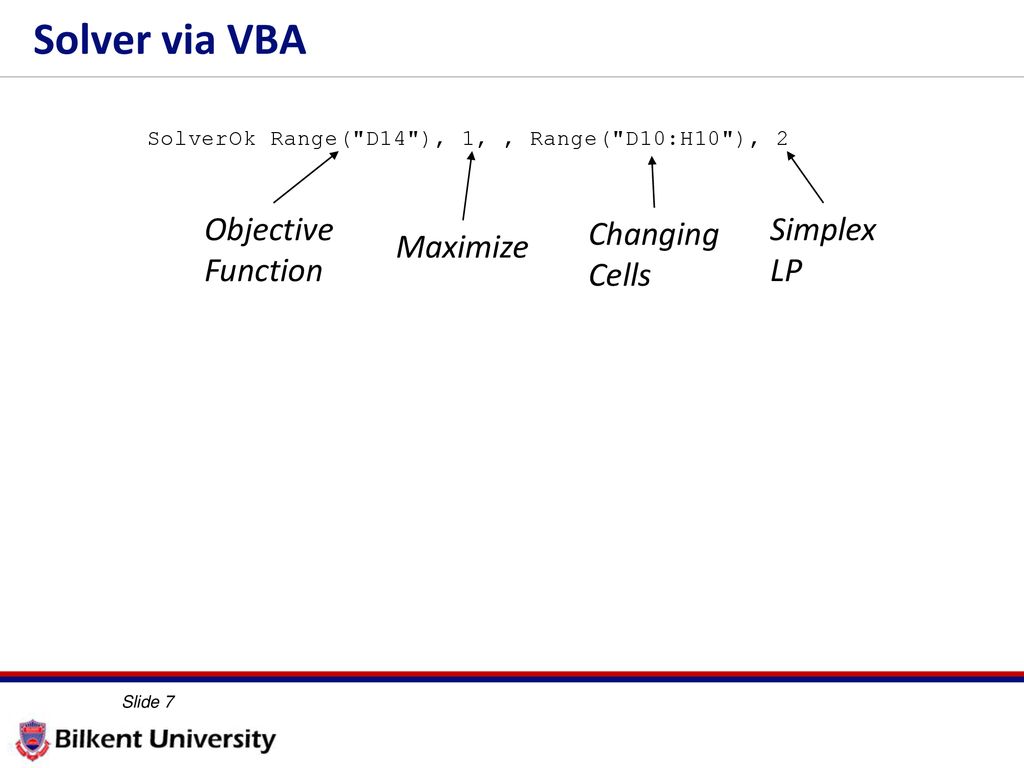
This example uses the Solver functions to maximize gross profit in a business problem. The SolverOK function defines a problem by specifying the SetCell, MaxMinVal, and ByChange arguments.
Simplex Lp Excel 2007
Support and feedback
Have questions or feedback about Office VBA or this documentation? Please see Office VBA support and feedback for guidance about the ways you can receive support and provide feedback.
